裁剪：裁剪部 JZsj9九游会官方

【新智元导读】LLM作念数学题，并非靠确凿推理，而是靠顾虑？最近，普林斯顿、谷歌等商榷者详备解剖了o1-mini等模子作念数学题的历程，发现它们靠的是记！最实锤的笔据之一，即是题目明明一经转变了条目，模子却依然给出了原题的谜底。

破案了！

就在刚刚，来自普林斯顿和谷歌的商榷者发现——

大模子作念数学题，不是靠推理，而是靠从西宾集里记下的解题手段！

这「未解之谜」一直困扰着不少业内东谈主士：在数学上，LLM到底是学会了举一反三，照旧仅仅学会了背题？

此前OpenAI o1-preview被爆出，数学题目稍作修改，正确率暴降30%！

之后，OpenAI用o3-mini讲解了LLM的坚定数学推明智商，但网上就稀疏据鸠合沟通类型的题目，让这一问题显得愈加扑朔迷离。

此次华东谈主商榷团队带来了新进展，推出了全新的MATH-Perturb测试基准，测试AI泛化智商到底怎么。

跟着LLM在MATH、OlympiadBench和AIME上连破记录，这让东谈主们看到了AI在数学领域的雄壮后劲。

「数学天才」头脑的背后，模子是竟然模子认知了数学学问、掌持了推理精髓，照旧仅仅名义上的「顾虑游戏」？

淌若模子在西宾时战役到了与测试集相似的题目，那它在测试中的高准确率可能就有「水分」，很可能仅仅记着了谜底，而非确凿认知了解题想路。

就像一个学生，靠死记硬背记着了讲义上的例题谜底，一朝考试题目稍有变化，就不知谈怎么下手。

商榷东谈主员采用零样本想维链（zero-shot chain-of-thought）的方法，对18种不同类型的LLM进行了全面测试。这些模子涵盖了长想维链模子、闭源大模子、开源小模子以及数学专用模子等。

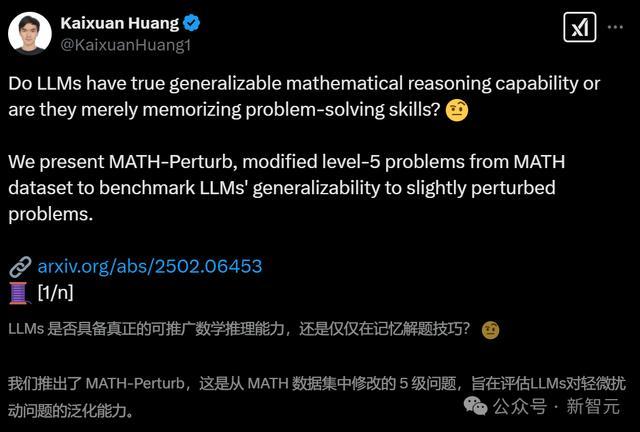
在MATH-P-Hard数据集上，测试的统统模子皆遭受了「滑铁卢」，准确率宽广镌汰了10%-25%，包括OpenAI的GPT-4/o1系列、谷歌的Gemini系列以及Deepseek-math、Qwen2.5-Math等模子。

著作的主要松手如下：

对18个LLM的数学推明智商进行了基准测试，松手夸耀统统模子，包括o1-mini和Gemini-2.0-flash-thinking，在MATH-P-Hard上的性能权臣着落（10%-25%）。这标明这些模子偏向于原始推理款式的散播，况且濒临硬扰动的问题时，会受到散播外效应的影响。

对失败款式分析的深刻分析，并发现了一种新的顾虑样式，即模子从西宾鸠合顾虑了解题手段，并在不判断修改后的缔造是否仍然适用的情况下盲目应用这些手段。

商榷了使用相应的原始未修改问题和管制决议进行高下体裁习ICL的影响，并讲解在MATH-P-Hard上，使用原始示例的ICL可能会损伤模子的推崇，因为模子可能无法识别渺小的各异，并被示例误导。

由12位商榷生级别的大众筹划、想象并构建了 MATH-P-Simple（粗造扰动）和 MATH-P-Hard（硬扰动）两个数据集，自MATH数据集的第5级（最难）问题。

这不由得让东谈主想起之前苹果商榷者的一篇广为流传的论文。

他们发现，给数学题换个皮，LLM本来会作念的数学题，就忽然不会了！

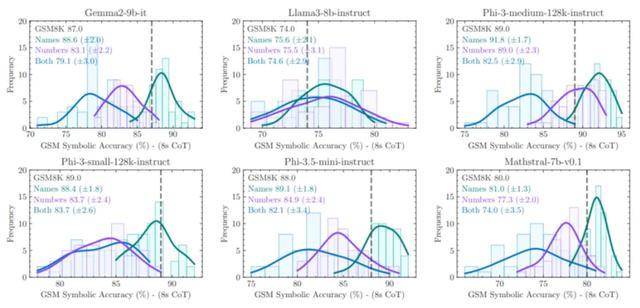
「当索菲护理她侄子时，她会为他拿出多样各类的玩物。积木袋里有31块积木。毛绒动物桶里有8个毛绒动物。堆叠环塔上有9个五彩纷呈的环。索菲最近买了一管弹性球，这使她为侄子准备的玩物总额达到了62个。管子里有若干个弹性球？」把这谈题中索菲的名字、侄子的称谓、玩物的具体数量转变，模子就作念不合了

只修改了题目中的私着名词，LLM的推崇就昭着出现了散播均值从右向左的移动，方差增多，也即是说，它们作念题的准确度变低了。

此次普林斯顿、谷歌的这项商榷，也再次考据了这篇论文的不雅点：LLM对数学题的推明智商，有水分。

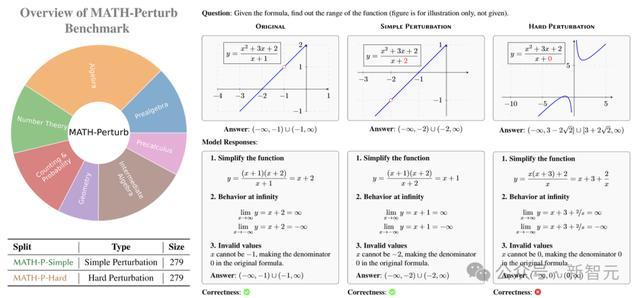
MATH-Perturb：数学推明智商的「试金石」

为了更准确地评估LLM的数学推明智商，商榷东谈主员推出了MATH-Perturb基准测试，用来考试模子在濒临不同难度扰动时的推崇。

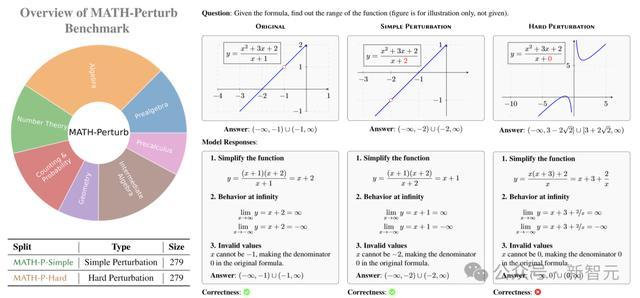
这个基准测试包含两个部分：MATH-P-Simple和MATH-P-Hard，题目均来自MATH数据鸠合难度最高的5级问题。

在构建数据集时，商榷东谈主员邀请了12位具有深厚数学配景的数学大佬来担任注视者。

关于MATH-P-Simple，注视者进行的是粗造扰动，对原问题进行一些非骨子的修改，举例转变问题中的数值、变量称号或表述样式，但不转变问题的基本推理款式妥协题方法。

比如，原问题是求函数

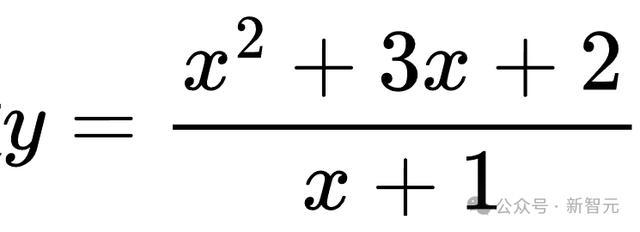
的值域，经过粗造扰动后，变成求

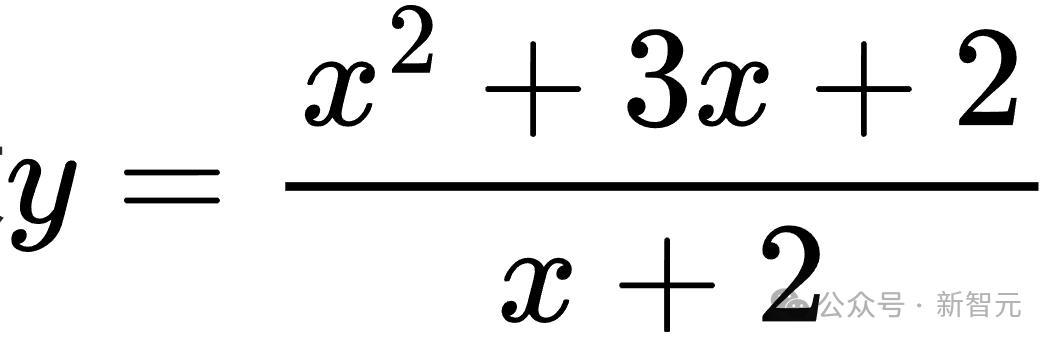
的值域。诚然题目有所变化，但解题的中枢想路照旧通过因式理解和分析函数特质来求解。

MATH-P-Simple和MATH-P-Hard的标注历程

硬扰动（MATH-P-Hard）则是对原问题进行小而要津的修改，这些修改会导致原有的解题方法不再适用，需要哄骗更高等的数学学问和更复杂的推理手段来管制。

通常以函数值域问题为例，硬扰动后的问题可能变成求

的值域，这时就需要哄骗柯西-施瓦茨不等式等更复杂的数学学问来求解。

竟然，这么修改后，LLM就通晓马脚了！

它们并莫得发现，原先我方学会的解题手段，并不适用于修改后的数学题，而是不时盲目套用。

比如这谈题中，数学题中具体条目转变后，模子仍然采用了原先的解法，最终天然就得出了诞妄的谜底。

（更多具体情况，参见实验松手）

此外，商榷东谈主员还恪守了两个紧迫原则。

「最小修改」原则要求注视者尽量减少对原问题的修改，这么能在保持问题样式把握的情况下，测试模子的泛化智商。

「谜底转变」原则保证修改后的问题谜底与原谜底不同，防卫模子告成输出顾虑中的谜底，确保松手真实可靠。

构建完数据集后，商榷东谈主员对每个扰动后的问题进行了仔细检查，确保问题的表述明晰、准确，况且谜底正确。

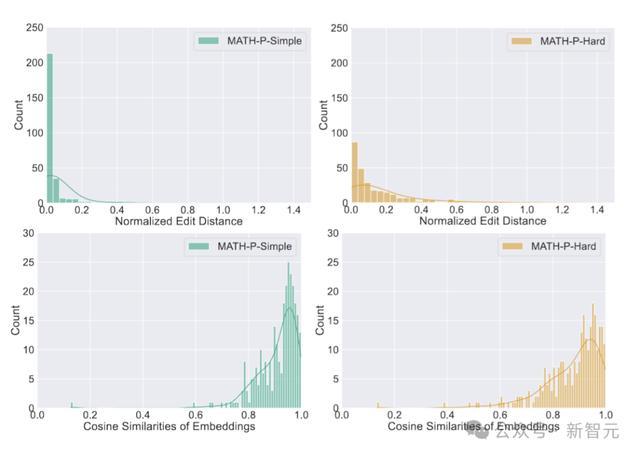
扰动问题与原始问题之间的归一化裁剪距离和镶嵌向量余弦相似度散播情况如下图所示。

详备松手

商榷东谈主员采用零样本想维链算作在基准测试中的方法评估方法。

为了进行对比，还会在原始的279个问题集上对模子进行评估，以下末节中将其称为「原始」(Original)。

测试不允许使用任何器用，包括拜谒代码解释器，因为发现好多问题不错通过编写暴力搜索方法松驰管制。

为了检查生成的谜底是否与真实谜底相匹配，采用了等价性检查方法：最初进行字符串法式化，然后使用sympy包检查两个数学对象的等价性。

LLM的基准测试性能

研究了多种说话模子，包括长想维链（long-CoT）模子、闭源的大型模子、开源的微型模子以及专门针对数学的模子。其中具体分类如下：

长想维链（long-CoT）模子：o1-preview，o1-mini，Gemini 2.0 flash thinking

闭源模子：GPT-4o，GPT-4 Turbo（Achiam等，2023），Gemini 1.5 Pro，Gemini 2.0 flash，Claude 3.5 Sonnet，Claude 3 Opus（Anthropic, 2024）

开源通用模子：Llama 3.1，Gemma 2，Phi-3.5

数学专用模子：MetaMath，MAmmoTH2，Deepseek-Math，Qwen2.5-Math，NuminaMath，Mathtral

下表阐明了LLM在原始问题集、MATH-P-Simple和MATH-P-Hard上的全体准确率，并分别经营了来自西宾集和测试集的准确率。

如预期的那样，评估的统统模子在MATH-P-Hard上的推崇权臣低于原始问题集，标明MATH-P-Hard愈加费劲。

同期，相较于原始问题集，大大批模子在MATH-P-Simple上的推崇也略有着落。

作家防卫到，性能着落主要来自西宾集。即便测试样本与西宾问题具有沟通的推理款式，起始进的模子也仍然存在泛化盘曲。

关于来自测试集的问题，空想情况下，原始问题和MATH-P-Simple修改版，对模子来说应当是通常「从未见过」的。

根据表1中的实考据据，不雅察到不同的松手：多个模子性能着落超越了5%；不外，令东谈主惊诧的是，Phi-3.5-mini-instruct的推崇反而有所升迁。关于评估的大大批模子，MATH-P-Simple测试集的准确率接近原始测试集的准确率。

值得一提的是，尽管已有商榷发现经过修改的基准与原始基准之间，模子的性能着落幅度为58%到80%（测试的最好模子是GPT-4），但在此次评估的模子中并未不雅察到如斯雄壮的差距，这标明新拓荒的模子在搪塞粗造扰动时的鲁棒性有所进展。

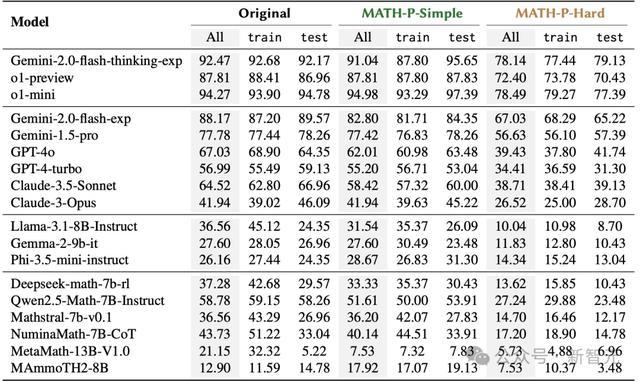
LLM零样本想维链性能准确率：「Orignal」指的是未修改的279个问题集。关于train列和test列，分别阐明来自西宾集和测试集的问题的准确率

推理本事膨胀。已有商榷标明，膨胀推理本事经营不错提高LLM的性能。将推理本事膨胀到基准测试的松手。

关于每个问题，孤苦生成N个解答，并通过以下公式经营每个1≤k≤N的pass@k策动：

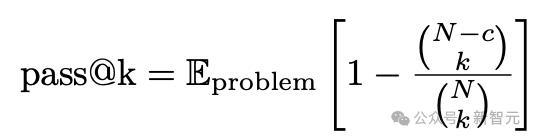
其中c是n次开动中正确谜底的数量。

此外，还经营了自一致性，即大批投票法的推崇。关于每个k，从N次开动中立时抽取k个复兴，并得到大批投票的谜底。

下图阐明了5次立时抽样的平均值和方法差。关于Llama-3.1-8B-Instruct和Qwen2.5-Math-7B-Instruct，缔造N = 64，而关于o1-mini，缔造N = 8。

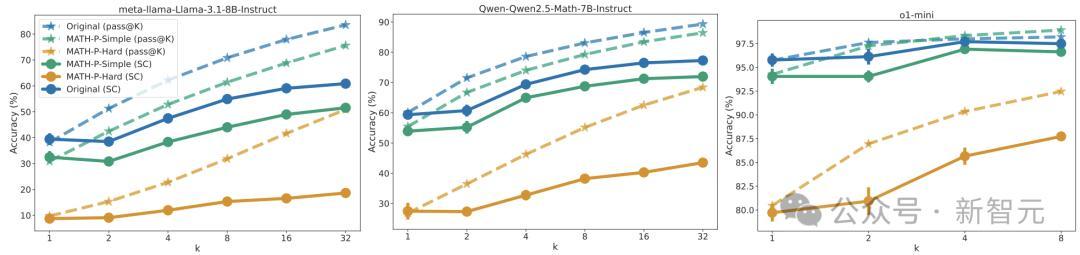
膨胀推理本事经营的成果

LLM作念数学题，会因为什么而失败

为了商榷模子在濒临硬扰动时的泛化智商，作家鸠合分析了那些在MATH-P-Hard修改版中的失败案例。

但要防卫：总问题中的20%-47%，模子至少能正确管制原始问题或MATH-P-Simple修改版。

关于这些问题，不错使用较容易问题的正确解算作参考，更好地详情模子在费劲问题中的失败款式。

最初，不雅察到当模子濒临更难的问题时，宽广存在一些失败款式。这些诞妄在较弱的模子中推崇得尤为凸起。

除了常见的失败款式外，当相比MATH-P-Hard修改版的诞妄解与较容易版块时，卤莽识别出一定数量的顾虑化问题。

具体来说，模子可能忽略修改后的假定，诞妄地假定原始假定仍然建树。

举例，参见图5中的示例。原问题为：

问题：十个东谈主围坐在一张圆桌旁。立时抽取其中三个东谈主作念演讲。被选中的三个东谈主坐在贯穿座位上的概率是若干？

修改后，问题变难了：

十个东谈主围坐在一个圆桌旁，立时聘请三个东谈主以特定轨则进行演讲。问这三个东谈主中，第一个和第二个演讲者坐在贯穿座位上，况且第二个和第三个演讲者也坐在贯穿座位上的概率是若干？

模子并没挑升志到问题一经转变，正本的推理方法不再有用。然后按照正本的推理款式进行推理，给出了原题的谜底——1/12。

而试验上，正确谜底是应该是1/36。

作家手动进行了20次近似发现Claude-3.5-Sonnet的通过率为50%。在诞妄中，30%是由于上述顾虑问题形成的。

顾虑化与诞妄推理结合的示例

在其他情况下，模子可能盲目地应用原始问题的解题手段，而莫得最初判断这些手段在修改后的问题环境中是否仍然适用（图1中的复兴即是由GPT-4o生成的一个例子）。

道理道理的是，模子以致可能输出原始问题的预期松手（并未在高下文中提供），而不是修改版问题的松手。

比如上头这谈题吧，原题是淌若

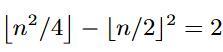
并找出统统得志条目的整数n。

而转变后的题将条目替换为

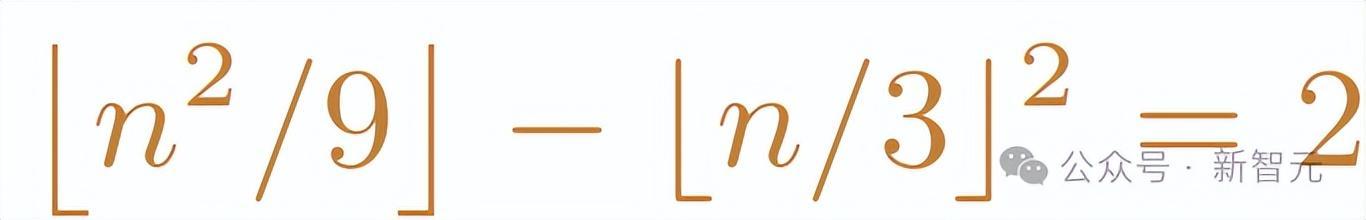
并要求找出得志条目的最小整数n。

松手在这种情况下，模子给出的谜底却是统统整数值（10和13），而非最小整数值（10）。

诶，这是模子背谜底实锤了？

要知谈，这种顾虑化步履关于大大批现存文件中的扰动类型来说是难以捕捉的，因为这些扰动并不需要不同的解题政策。

款式崩溃

商榷东谈主员还和顺了款式崩溃（pattern collapse）带来的影响。

款式崩溃是指模子无法离别扰动后的问题和原问题，导致复兴与原问题谜底沟通。

在MATH-P-Hard数据鸠合，除了少数几个模子外，款式崩溃的情况在总诞妄中的占比不到10%。

这标明，模子在濒临硬扰动问题时，诚然可能会出现多样诞妄，但大批情况下照旧卤莽意志到问题的变化，而不是粗造地重收复谜底。

接洽词，东谈主工检查发现，模子的输出频频不是粗造地重收复谜底，而是在推理历程中出现了一些玄妙的诞妄，举例忽略或污蔑修改后的假定。

高下体裁习

高下体裁习是指模子在推理时利用原问题和谜底算作示例来扶持解题。

在MATH-P-Simple数据集上，使用原问题和谜底算作高下体裁习示例，简直能升迁统统模子的性能。

这是因为MATH-P-Simple问题不错通过告成应用原解题门径来管制，原问题和谜底的示例能提供有用的足迹。

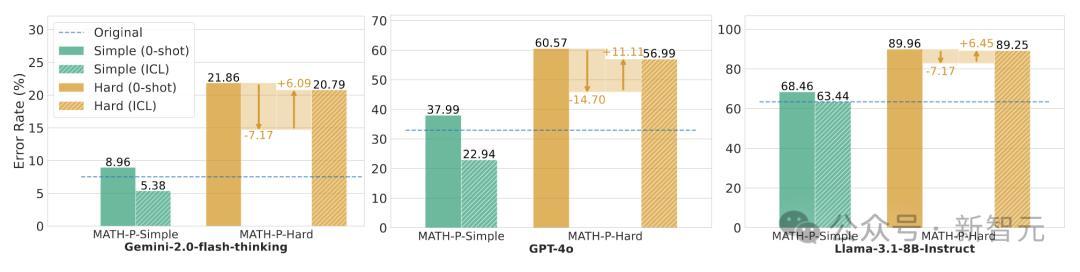
接洽词，在MATH-P-Hard数据集上，高下体裁习的成果则较为复杂。

诚然原谜底中的数学学问或然卤莽匡助模子管制修改后的问题，但由于原问题和MATH-P-Hard问题之间存在玄妙的各异，模子也容易被原谜底误导，导致诞妄增多。

总体来看，高下体裁习在MATH-P-Hard上的成果并不睬想，升迁幅度相配有限。

LLM在濒临硬扰动问题时，推崇出昭着的局限性，好多诞妄源于模子对解题手段的盲目顾虑，而短缺对问题骨子的认知。

总之，这项商榷夸耀，统统模子在复杂扰动MATH-P-Hard 上的推崇均有所着落，而且好多诞妄皆是源于一种新的顾虑样式——

模子从西宾鸠合记着了解题手段，然后在题目转变条目后，并不判断是否适用，而盲目应用这些手段。

这证实，诚然大大批LLM在数学推理方面获取了一定的获利，但距离确凿认知和掌持数学学问还有很大的差距。

不外最近，谷歌DeepMind拿下IMO金牌的AlphaGeometry，初度破解了2009年IMO最难几何题G7。

在历程中，它给出了震天动地的惊东谈主解法——

利用要津的扶持作图（图中的红点），就只需求「角度」和「比例推导」。

是以，o1-preview、o1-mini、GPT-4o、Deepseek-Math等模子，在解数学题上和AlphaGeometry究竟进出多远呢？

这就让东谈主十分期待j9九游会官方，接下来这个领域的更多商榷了。